Many logistic activities are concerned with linking material flows among companies and processes. In such applications, we find a combination of quantity decisions, e. g. the amount of goods shipped (Inventory Management), and routing decisions as tackled in the area of Vehicle Routing. Clearly, both areas intersect to a considerable degree, complicating the solution of such problems. Recently, intensive research has been conducted in this context which is commonly refereed to as Inventory Routing Problems (IRP). Several variants of the IRP can be found, ranging from deterministic demand cases to stochastic models.
From the practical point of view of the companies, reality is much more complex than a know demand and much more uncertain than a stochastic law. In fact, companies often have a partial knowledge of the demand over the planning horizon. Our observation of this phenomenon can be transformed in a new type of data, which we propose for further experimental investigations. We here assume that demand of the current period is known at the beginning of the period. Besides, we have an approximate overview of the demand over the 5 next periods, the 20 next periods and the 60 next periods. This overview is rather good (e.g. it does not differ from reality by more that ±10%) but of course, we cannot predict with certainty what will happen the next periods.
The global objective of this work is to provide practical optimization methods to companies involved in inventory routing problems, taking into account this new type of data. Also, companies are sometimes not able to deal with changing plans every period and would like to adopt regular structures for serving customers.
As our work is a long term project, we are gradually going to develop our solution approach. In a first phase, we will focus on the Inventory Routing problem with a single product, deterministic known demand over a finite horizon. We assume that the routing costs and the inventory costs are not comparable and therefore should be handled as two different objectives. To our knowledge, this is the first time that a bi-objective approach is considered for this problem.
We consider a distribution network (usually a complete graph or a distance matrix) where a single product is shipped from a depot (denoted by 0) of unlimited capacity to a set C={1,…,n} of customers over a time finite horizon H of p periods. A homogeneous fleet of trucks of capacity K serves the customers (the number of trucks that can be used at every time period is not limited). Alternatively, a single truck can be used to do several tours over the same period. Each customer i has a maximum capacity Ui and an initial inventory level Ii0. The goal is to minimize two cost functions, namely the total routing costs (the sum of routing costs in each period) and the total inventory costs (the sum of the inventory levels at the end of each period for all customers).
Proposed benchmark instances
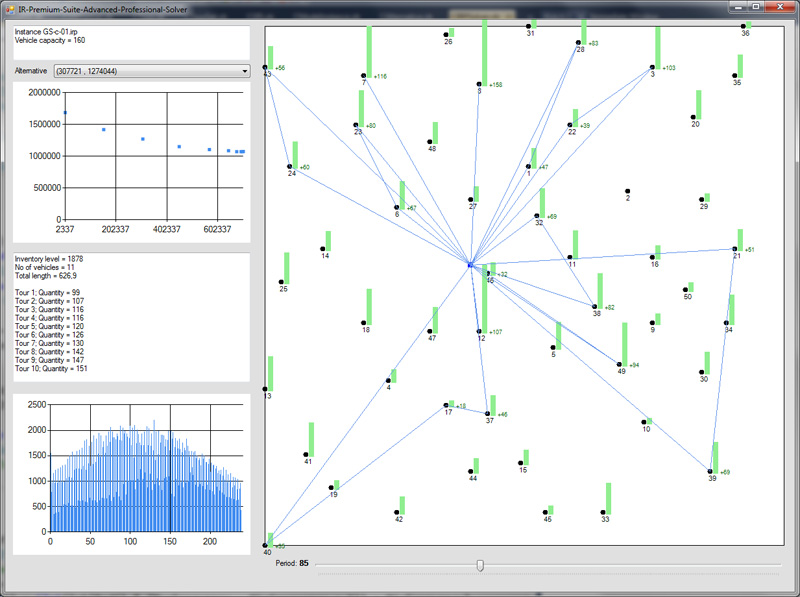
Preview of the IRP Solver software
Scientific Collaborators
This is joint work with Prof. Marc Sevaux, PhD.
Related key publications

Sandra Huber, Martin Josef Geiger and Marc Sevaux (2015):
Interactive Approach to the Inventory Routing Problem: Computational Speedup Through Focused Search.
In Jan Dethloff, Hans-Dietrich Haasis, Herbert Kopfer, Herbert Kotzab and Jörn Schönberger (editors): Logistics Management, Volume of the series Lecture Notes in Logistics, Pages 339–353, Springer International Publishers, ISBN 978-3-319-13177-1.
[doi.:10.1007/978-3-319-13177-1_27]
 Martin Josef Geiger and Marc Sevaux (2011):
Martin Josef Geiger and Marc Sevaux (2011):
The biobjective inventory routing problem – problem solution and decision support.
In Julia Pahl, Torsten Reiners and Stefan Voß (editors): Network Optimization, Volume 6701 of the series Lecture Notes in Computer Science, Pages 365–378, Springer Verlag, Berlin, Heidelberg, ISBN 978-3-642-21526-1.
[doi:10.1007/978-3-642-21527-8_41]
Letzte Änderung: 26. November 2017