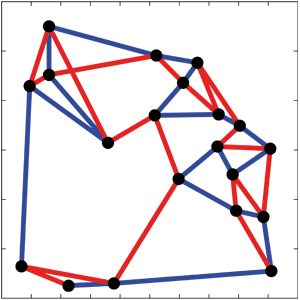
Some of our research activities are devoted to disjoint path planning (DPP). In DPP, a graph G=(V,E) is given, within which a set of disjoint paths/routes has to be found such that some objective function, for example the maximum length of all constructed paths, is minimized. Applications of disjoint path planning problems are found in logistics, where several distinct vehicle routings have to be found. Here, disjoint paths/ routes provide a degree of flexibility, and also ensure that vertices are not visited in the same order every day. Especially in security critical applications, such as the routing of security firms, this property can be of upmost importance.
The figure on the left depicts two edge-disjoint paths within a graph G. Obviously, each node is visited by the red and the blue path, while both paths do not share a common edge.
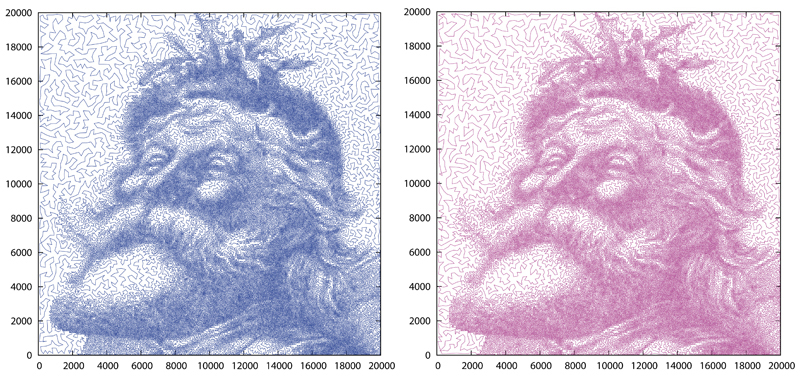
A variant of the problem was introduced December 2012–January 2013 in the Kaggle Competition on the „Traveling Santa Problem“. In this setting, two edge-disjoint Hamiltonian paths had to be found for a graph consisting of 150,000 nodes, minimizing the length of the longer path.
Our algorithm/ computer implementation ranked 19th in this international competition (out of 356 registered teams), with a final objective function value of 0.7% above the best-known solution.
The following two figures illustrate the two computed paths for the 150,000 nodes-dataset. Although the look similar (in fact they are of similar length), they are edge-disjoint.
Letzte Änderung: 26. November 2017